Modeling proportion/binary data

GLM for proportion/binary data

  • Logistic regression is binomial glm with logistic links
  • When to use binomial regression / quansi binomial regression / beta regression / beta binomial regression ?

Gamma regression

The parametrization of gamma distribution

  • Gamma distribution commonly has two type of parametrization
    • Shape \(\alpha\) and rate \(\beta\)
    • Shape \(k\) and scale \(\theta\)
    • Rate and shape follows \(\theta=1/\beta\)
  • In GLM, the mean \(\mu = \alpha/\beta = \alpha\theta\) and shape \(\alpha\) parametrization was used
  • The Gamma GLM in both R and python statsmodel assume constant shape \(\alpha\), and inverse of \(\alpha\) is called dispersion \(\phi=1/\alpha\)
  • In statsmodels, scale has a distinct meaning, the estimated dispersion \(\phi=1/\alpha\) called scale
    • The actual scale \(\theta\) can be calculated from model’s predicted mean \(\mu\)
  • MASS package provide more precised estimation of the fixed shape patrameter

Simulate data

  • In the following setting
    • fixed shape \(\alpha=2\)
    • intercept is 0.5
    • cofficient is 0.8
    ## Import packages 
import statsmodels.api as sm
import matplotlib.pyplot as plt 
import scipy.stats as stats 
import numpy as np

# Generate data
np.random.seed(1)
x=np.random.uniform(0,100,50000)
mask = (x>50)
x[mask],x[~mask] = 1,0
x2 = sm.add_constant(x)
a,b = 0.5,0.8
y_true = a+b*x
# Add error 
shape = 2 
scale = y_true/shape 
y = np.random.gamma(shape=shape, scale=scale)
    • Histogram of simulated data
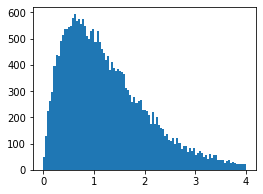
    • image
  • Fit glm model 
    # Fit gamma glm with identity link function
glm =  sm.GLM(y, x2, family=sm.families.Gamma(sm.genmod.families.links.identity()))
model = glm.fit()
  • The estimated shape parameter 
    1/model.scale # 1.9845020937600035 ~ 2
  • Simulate data when covariate is 1 using the fitted parameters
    • model.predict generate predicted \(\mu\)
    shape = 1/model.scale
mean = model.predict(exog=np.array([[1,1]]))
scale = mean/shape
x1_pred = np.random.gamma(shape=shape, scale=scale,size=y[mask].shape[0])
    • Histogram of predicted data
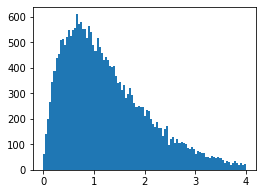
    • image

Doing Similar Things in R

  • Simulate data with known parameter and fit with GLM
  # Fit gamma glm with simulated data
  set.seed(1)
  x <- runif(50000, min = 0, max = 100)
  mask <- (x>50)
  x[mask] = 1;x[!mask] = 0
  a <- 0.5;b <- 0.8
  y_true <- a + b * x
  shape <- 2
  scale <- y_true/shape
  y <- rgamma(n = length(x), shape = shape, scale = scale)
  gamma.glm <- glm(y ~ x, family = Gamma(link = "identity"))

  # Cofficient in glm.summarized should nearly idetical to the simulation setting
  glm.summarized <- summary(gamma.glm)
  shape.hat.glm <- 1/glm.summarized$dispersion

  # MASS use MLE to get shape estimation claimed to be more accurate
  library(MASS)
  shape.hat.mass <- MASS::gamma.shape(gamma.glm)$alpha

  # Sampling data from fitted model
  N <- 1000
  rate <- shape.hat.mass/predict(gamma.glm,data.frame(x=c(1.3)))
  sampled <- rgamma(N,rate=rate,shape=shape.hat.mass)

Difference between Bernoulli vs. Binomial Response in logit model

Statistical testing for methylation data

Reference