• 看了不知道多少遍总是记不清楚，详细记录一下，希望别再忘了:)

EM algorithm for motif finding

  • Input data: \(n\) sequences \(X_1,X_2,...,X_n\) with different lengths
  • Find ungapped motif with fixed length \(w\)
  • \(\theta\) is the motif paramter and background paramater
  • There are \(m_i=L_i-w+1\) possible staring position in sequence \(X_i\) with length \(L_i\)
  • \(Z_{ij}\) is a binary indicator variable, indicate whether there is a motif start at position \(j\) in sequence \(i\)
  • Denote number of motifs in sequence \(i\) as \(Q_i=\sum_{j=1}^{m_i}Z_{ij}\).
  • A sequence may contains 0 motifs, 1 motifs or more than one motifs.

OOPS

  • assume one occurrence per sequence

  • Likelihood of a sequence given the motif position

\[\log P(X_i \mid Z_{ij}=1,\theta) = \sum_{k=0}^{w-1}I(i,j+k)^T \log p_k + \sum_{k \in \Delta_{i,j}}I(i,k)^T \log p_0\]
  • Prior probability that \(Z_{ij}=1\) (motif in sequence \(i\) starts at \(j\))
\[P(Z_{ij} \mid \theta) = \frac{1}{m_i}\]
  • Joint likelihood of sequence and motif start pisition for each seuence
\[P(X_i,Z_i|\theta)=P(X_i|Z_i,\theta)P(Z_i|\theta)=\prod_{j=1}^{m_{i}}[P(X_i|Z_{ij}=1,\theta)P(Z_{ij}=1|\theta)]^{Z_{ij}}\]
  • Joint log likelihood for each seuence
\[\begin{align*} \log P(X_i,Z_i \mid \theta) &=\sum_{j=1}^{m_{i}}Z_{ij}\log P(X_i|Z_{ij}=1,\theta)+\sum_{j=1}^{m_{i}}Z_{ij}\log P(Z_{ij}=1|\theta) \\ &=\sum_{j=1}^{m_{i}}Z_{ij}\log P(X_i|Z_{ij}=1,\theta)+ \log \frac{1}{m_i} \\ \end{align*}\]
  • EM for motif finding. Denote model paramters at step \(t\) as \(\theta^{(t)}\) s
  • E step: calculate \(\mathbb{E}_{Z_{ij} \mid X_i,\theta^{(t)}} Z_{ij}\),
\[\begin{align*} \mathbb{E}_{Z_{ij} \mid X_i,\theta^{(t)}} Z_{ij} &= 1*P(Z_{ij}=1 \mid X_i,\theta^{(t)})+0*P(Z_{ij}=0 \mid X_i,\theta^{(t)}) \\ &=P(Z_{ij}=1 \mid X_i,\theta^{(t)}) =\frac{P(X_i,Z_{ij}=1 \mid \theta^{(t)})}{P(X_i \mid \theta^{(t)})} \\ &=\frac{P(X_i,Z_{ij}=1 \mid \theta^{(t)})}{\sum_{k=1}^{m}P(X_i,Z_{ij}=1 \mid \theta^{(t)})} \\ &=\frac{P(X_i \mid Z_{ij}=1,\theta^{(t)})P(Z_{ij}=1 \mid \theta^{(t)})}{\sum_{k=1}^{m}P(X_i \mid Z_{ik}=1,\theta^{(t)})P(Z_{ik}=1 \mid \theta^{(t)})} \\ &=\frac{P(X_i \mid Z_{ij}=1,\theta^{(t)})}{\sum_{k=1}^{m}P(X_i \mid Z_{ik}=1,\theta^{(t)})} \end{align*}\]
  • M step: replace \(Z_{ij}\) in \(\log P(X_i,Z_i \mid \theta)\) with \(\mathbb{E}_{Z_{ij} \mid X_i,\theta^{(t)}} Z_{ij}\), perform standard MLE to update \(\theta^{(t)}\) to \(\theta^{(t+1)}\)

ZOOPS

  • assume zero or one motif occurrences per dataset sequence), add parameter \(\gamma\), probability that a sequence contains a motif. \(\lambda_i=\frac{\gamma}{m_i}\) is prior probabaility that any position in a sequence is start of a motif

  • Likelihood of a sequence contain one motif, given the motif position is same as OOPS

  • Likelihood of a sequence without a motif

\[P(X_i \mid Q_i=0,\theta) = \prod_{k=1}^{L}p_{X_{i,k},0}\]
  • Joint likelihood of sequence and motif start pisition for each seuence
\[P(Q_i \mid \theta, \gamma) = \gamma^{Q_i}(1-\gamma)^{1-Q_i}\] \[P(Z_{ij}=1 \mid Q_i=1, \theta)=\frac{1}{m_i}\]
  • Joint log-likelihood
\[\begin{align*} P(X_i,Z_i|\theta,\gamma)&=P(X_i,Z_i,Q_i|\theta,\gamma)\\ &=P(Q_i|\theta,\gamma)P(X_i,Z_i|Q_i,\theta,\gamma) \\ &=(1-\gamma)^{1-Q_i}P(X_i \mid Q_i=0)^{1-Q_i}\gamma^{Q_i}\prod_{j=1}^{m_{i}}[P(Z_{ij}=1 \mid Q_i=1,\theta)P(X_i \mid Z_{ij}=1,Q_i=1,\theta)]^{Z_{ij}} \\ &=(1-\gamma)^{1-Q_i}P(X_i \mid Q_i=0)^{1-Q_i}\gamma^{Q_i}\prod_{j=1}^{m_{i}}[\frac{1}{m_i} P(X_i \mid Z_{ij}=1,\theta)]^{Z_{ij}} \end{align*}\] \[\begin{align*} \log P(X_i,Z_i|\theta,\gamma)&=Q_i \log \frac{\gamma}{m_i} + (1-Q_i )\log (1-\gamma) + (1-Q_i) \log P(X_i|Q_i=0) \\ & + \sum_{j=1}^{m_{i}}Z_{ij}\log P(X_i|Z_{ij}=1,\theta) \end{align*}\]

  • EM for motif finding

  • E step: calculate \(\mathbb{E}_{Z_{ij} \mid X_i,\theta^{(t)}} Z_{ij}\)

\[\begin{align*} \mathbb{E}_{Z_{ij} \mid X_i,\theta^{(t)}} Z_{ij} &= P(Z_{ij}=1 \mid X_i,\theta^{(t)}) = \frac{P(X_i,Z_{ij}=1 \mid \theta^{(t)})}{P(X_i \mid \theta^{(t)})} \\ &= \frac{P(X_i,Z_{ij}=1 \mid \theta^{(t)})}{P(X_i, Q_i=0 \mid \theta^{(t)}) + P(X_i, Q_i=1 \mid \theta^{(t)})} \\ &= \frac{\frac{\gamma}{m_i} P(X_i \mid Z_{ij}=1,\theta^{(t)})}{P(X_i \mid Q_i=0, \theta^{(t)})(1-\gamma) + \frac{\gamma}{m_i} \sum_{k}^{m_i} P(X_i \mid Z_{ik}=1, \theta^{(t)})} \end{align*}\]

TCM

  • two component mixture, motif can start at any feasible positions

  • Joint likelihood of sequence and motif start pisition for each seuence \(\begin{align*} P(X_i,Z_i|\theta,\lambda)&=P(X_i,Z_i|\theta,\lambda)\\ &=\prod_{j=1}^{m_i}\lambda^{Z_{ij}}(1-\lambda)^{1-Z_{ij}}P(X_{ij} \mid Z_{ij}=1)^{Z_{ij}}P(X_{ij} \mid Z_{ij}=0)^{1-Z_{ij}} \end{align*}\)

  • Joint log-likelihood \(\begin{align*} \log P(X_i,Z_i|\theta,\lambda) = \sum_{j=1}^{m} [Z_{ij} \log \lambda +(1- Z_{ij}) \log (1-\lambda) + (1-Z_{ij}) \log P(X_{ij} \mid Z_{ij}=0) + Z_{ij} \log P(X_{ij} \mid Z_{ij}=1)] \end{align*}\)

HMM

  • \(N\) is length of the observation

  • \(n\) is number of hidden states

  • Hidden state \(Q\):

\[q_{1},q_{2},...,q_{t},...q_{N}\]
  • Emitted symbol \(O\):
\[o_{1},o_{2},...,o_{t},...,o_{N}\]

  • Transition probability matrix \(A_{N \times N}\). \(a_{st} = A_{st}\) is transition probability from state \(s\) to \(t\)

    \[a_{st} = P(q_{i}=t \mid q_{i-1}=s)\]

  • Initial probability distribution of hidden states \(\pi\) or transition probability from a slilent starting state to state \(p_i\)

\[\pi_{1},\pi_{2},...,\pi_{t},...\pi_{N}\]
  • Probability of emitting symbol \(b\) at state \(k\)
\[e_{k}(b)=P(x_{i}=b \mid q_{i}=k)\]

Forward algorithm (inference)

  • Determine the likelihood of an observed series, marginalized for all possible hidden states
  • Define the forward variable \(\alpha_{t}(j)\), that is given model parameter, the joint probability of being state \(j\) at time \(t\) with observation series \(o_1,o_2,...,o_t\)
\[\alpha_{t}(j)=P(o_1,o_2,...,o_t,q_t=j \mid \lambda)\]
  • We have (\(\lambda\) is omitted)
\[\begin{align*} P(o_1,o_2,...,o_t,q_t=j) =& \sum_{i=1}^{N} P(o_1,o_2,...,o_{t-1},o_t,q_{t-1}=i, q_t=j) \\ =& \sum_{i=1}^{N} P(o_1,o_2,...,o_{t-1},q_{t-1}=i \mid \lambda)P(q_t = j \mid q_{t-1}=i)P(o_t \mid q_t = j) \\ =& \sum_{i=1}^{N} \alpha_{t-1}(i)a_{ij} e_{i}(o_t) \end{align*}\]
  • Initialization
\[\alpha_{1}(j)= \pi_{j}e_{j}(o_1)\]
  • \(\alpha_{t}(j)\) can be determined by dynamic programming
\[\alpha_{t}(j)=\sum_{i=1}^{N} \alpha_{t-1}(i)a_{ij} e_{i}(o_t)\]
  • Marginalize across last hidden state
\[P(O|\lambda) = \sum_{i=1}^{N}\alpha_{T}(i)\]

Viterbi algorithm (decoding)

  • Find the most probable path of hidden states, given the model and observation

  • Define the Viterbi variable

\[V_{t}(j)=\max_{q_1,q_2,...,q_{t-1}}P(o_1,o_2,...,o_t,q_t=j \mid \lambda)\]
  • The intialization is same as forward algorithm
\[V_{1}(j)= \pi_{j}e_{j}(o_1)\]
  • A dynamic programming similar to forward algorithm (the difference is replace \(\sum\) operator with \(\max\) operator) is used to calculate viterbi variable
\[V_t(j)=\max_{i=1}^{N}V_{t-1}(i)a_{ij} e_{i}(o_t)\]
  • Keep track of the “best” hidden state, main a backtrace pointer matrix

Model training

  • Estimation HMM parameter from observations

Baum–Welch algorithm: forward-backward algorithm based, EM style training

  • Define backward variable \(\beta_{t}(i)\)
\[\beta_{t}(i)=P(o_{t+1},o_{t+2},...,o_{T}|q_{t}=i,\lambda)\]
  • Similar to forward variable, we have
\[\begin{align*} P(o_{t+1},o_{t+2},...,o_{T}|q_{t}=i) =& \sum_{j=1}^{N} P(o_{t+1},o_{t+2},...,o_T,q_{t+1}=j \mid q_t=i) \\ =& \sum_{j=1}^{N} P(o_{t+1},o_{t+2},...,o_T \mid q_{t+1}=j, q_t=i) P(q_{t+1}=j \mid q_{t}=i) \\ =& \sum_{j=1}^{N} P(o_{t+1},o_{t+2},...,o_T \mid q_{t+1}=j) P(q_{t+1}=j \mid q_{t}=i) \\ =& \sum_{j=1}^{N} P(o_{t+2},...,o_T \mid q_{t+1}=j) P(o_{t+1} \mid q_{t+1}=j) P(q_{t+1}=j \mid q_{t}=i) \\ = & \sum_{j=1}^{N} \beta_{t+1}(j) e_{j}(o_{t+1}) a_{ij} \end{align*}\]

  • We can use backward algorithm as an alternative to forward algorithm for calculating \(P(O \mid \lambda)\)

  • Initialization (last observation in each instance always transit to ending state with probability 1 regardless of the hidden state \(q_T\))

\[\beta_{T}(i) = 1\]
  • Recursion
\[\beta_{t}(i)=\sum_{j=1}^{N} \beta_{t+1}(j) e_{j}(o_{t+1}) a_{ij}\]
  • Termination (exact same as the recursion fumula if we add a silent starting state corresponds to \(t=0\))
\[P(O|\lambda)=\sum_{j=1}^{N} \beta_{1}(j)e_{j}(o_{1})\pi_j\]
  • The forward-backward algorithm
\[\hat{a}_{ij} = \frac{E(count\,of\,i \Rightarrow j\,transitions)}{E(count\,of\,i \Rightarrow .\,transitions)}\]
  • To compute such expectation, we define a forward-backward variable
\[\xi_{t}(i,j)=P(q_t=i,q_{t+1}=j \mid O,\lambda)\]
  • Note
\[\begin{align*} P(q_t=i,q_{t+1}=j, O\mid \lambda) =&P(o_1,o_2,...,o_t,q_t=j \mid \lambda) \\ &(q_{t+1}=j|q_t=i)P(o_{t+1}|q_{t+1}=j) \\ &P(o_{t+2},...,o_{T}|q_{t+1}=i,\lambda) \\ =&\alpha_{t}(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j) \\ \end{align*}\] \[\begin{align*} P(O\mid \lambda) =& \sum_{j=1}^{N} P(O,q_t =j \mid \lambda) \\ =& P(o_1,o_2,...,o_t,q_t=j \mid \lambda) \\ &P(o_{t+1},o_{t+2},...,o_{T} \mid q_{t}=j,\lambda) \\ =& \alpha_{t}(j)\beta_{t}(j) \end{align*}\]
  • Hence
\[\begin{align*} \xi_{t}(i,j) =& P(q_t=i,q_{t+1}=j \mid O,\lambda) \\ =& \frac{P(q_t=i,q_{t+1}=j, O\mid \lambda)}{P(O \mid \lambda)} \\ =& \frac{\alpha_{t}(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{\sum_{j=1}^{N}\alpha_{t}(j)\beta_{t}(j)} \end{align*}\]

Profile HMM

  • A spacial HMM primarily used for protein homolog modeling

  • The hidden states in a profile HMM for local alignment, with N key positions
    • start state
    • insertion state 0, modeling left flanking background sequence
    • match state at key position 1, insertion state at key position 1, deletion state at key position 1
    • …
    • match state at key position N, insertion state at key position N (modeling right flanking background sequence), deletion state at key position N
    • end state
  • Possible transitions
    • begin \(\Rightarrow\) insertion state 0
    • begin \(\Rightarrow\) deletion state at key position 1 (allow condition when first residue is missing)

    • begin \(\Rightarrow\) match state at key position 1

    • insertion state 0 \(\Rightarrow\) insertion state 0
      • self looping for left flanking background sequence modeling
      • The looping probability on the flanking states should be close to 1, since they must account for long stretches of sequence
    • insertion state 0 \(\Rightarrow\) deletion state at key position 1

    • insertion state 0 \(\Rightarrow\) match state at key position 1

    • match state at key position i-1 \(\Rightarrow\) match state at key position i
    • insertion state at key position i-1 \(\Rightarrow\) match state at key position i

    • deletion state at key position i-1 \(\Rightarrow\) match state at key position i

    • match state at key position i-1 \(\Rightarrow\) deletion state at key position i
    • insertion state at key position i-1 \(\Rightarrow\) deletion state at key position i

    • deletion state at key position i-1 \(\Rightarrow\) deletion state at key position i

    • match state at key position i \(\Rightarrow\) insertion state at key position i
    • insertion state at key position i \(\Rightarrow\) insertion state at key position i
    • deletion state at key position i \(\Rightarrow\) insertion state at key position i
      • “We have added transitions between insert and delete states, as they did, although these are usually very improbable. Leaving them out has negligible effect on scoring a match, but can create problems when building the model from MSA”
      • In most cases, profile HMM is constructed from MSA. Consider Figure 5.7 in Biological Sequence Analysis. We can see given a column assignment for MSA, the \(D_i \Rightarrow I_i\) transition could occur

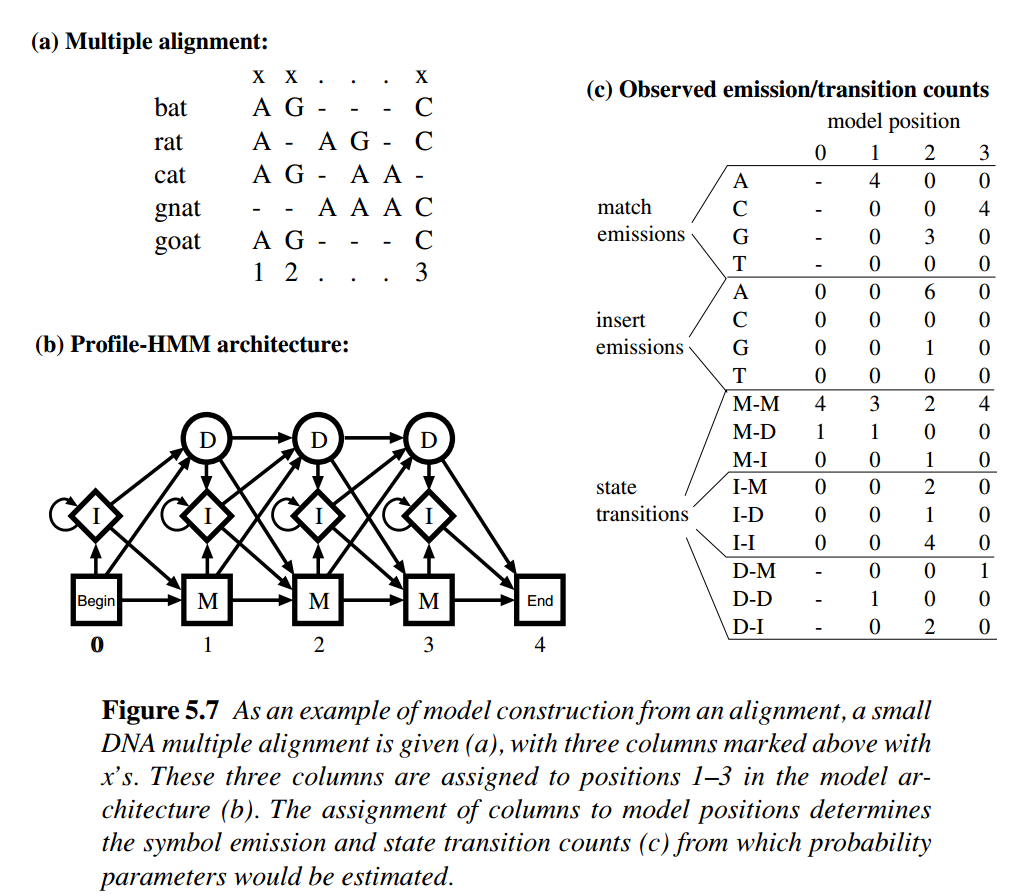
  • match state at key position i \(\Rightarrow\) end
  • insertion state at key position i \(\Rightarrow\) end
    • self looping for right flanking background sequence modeling, should be close to 1

  • deletion state at key position i \(\Rightarrow\) end

  • HMM Profile searching
    • Viterbi algorithm and forward algorithm can both be used for HMM profiling searching
    • Viterbi: assign a mostly likely hidden state for each nucleotide, and report the corresponding likelihood
    • Viterbi variable for matching, insertion and deletion states at key position j and sequence position i
\[\begin{equation} V_j^M(i) = \log{\frac{e_{M_j}(x_i)}{q_{x_i}}} + max \left\{ \begin{aligned} V_{j-1}^M(i-1) + \log a_{M_{j-1}M_j} \\ V_{j-1}^I(i-1) + \log a_{I_{j-1}M_j} \\ V_{j-1}^D(i-1) + \log a_{D_{j-1}M_j} \\ \end{aligned} \right. \end{equation}\] \[\begin{equation} V_j^I(i) = \log{\frac{e_{I_j}(x_i)}{q_{x_i}}} + max \left\{ \begin{aligned} V_{j}^M(i-1) + \log a_{M_{j}I_j} \\ V_{j}^I(i-1) + \log a_{I_{j}I_j} \\ V_{j}^D(i-1) + \log a_{D_{j}I_j} \\ \end{aligned} \right. \end{equation}\] \[\begin{equation} V_j^D(i) = max \left\{ \begin{aligned} V_{j-1}^M(i) + \log a_{M_{j-1}D_j} \\ V_{j-1}^I(i) + \log a_{I_{j-1}D_j} \\ V_{j-1}^D(i) + \log a_{D_{j-1}D_j} \\ \end{aligned} \right. \end{equation}\]

Model construction

  • To construct profile HMM from MSA, we have to make a decision. Each column in the MSA should either be assigned to a key position (marked column), or an insertion (unmarked column).
  • For columns marked as key positions, residues are assigned to match state, gaps are assigned to deletion state
  • For columns marked as insertions, residues are assigned to insertions, gaps are ignored
  • There are \(2^L\) ways to mark a MSA with \(L\) columns.
  • Three ways for marking MSA columns
    • Manual
    • Heuristics: rule based assignment. For example, assigning all columns will more than a certain fraction of gap characters to insert states
    • MAP (maximum a posteriori)